Summary

In summary, we have defined the following terms from the analysis of finite-difference schemes for the linear shift-invariant case with constant sampling rates:

• PDE well posed 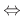$\Leftrightarrow$ PDE at least marginally stable
• FDS consistent 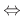$\Leftrightarrow$ FDS shift operator 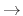$\to$ PDE operator as $T,X\to0$
• FDS stable 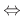$\Leftrightarrow$ stable or marginally stable as a digital filter
• FDS strictly stable 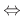$\Leftrightarrow$ stable as a digital filter
• FDS marginally stable 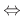$\Leftrightarrow$ marginally stable as a digital filter

Finally, the Lax-Richtmyer equivalence theorem establishes that well posed + consistency + stability implies convergence, where, as defined in §D.2 above, convergence means that solutions of the FDS approach corresponding solutions of the PDE as $T,X\to0$ .