Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Let 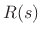 denote the driving-point impedance of an arbitrary
continuous-time LTI system. Then, by definition,
denote the driving-point impedance of an arbitrary
continuous-time LTI system. Then, by definition,
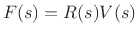 where
where 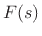 and
and  denote the Laplace transforms
of the applied force and resulting velocity, respectively.
The wave variable decomposition in Eq.(C.74) gives
denote the Laplace transforms
of the applied force and resulting velocity, respectively.
The wave variable decomposition in Eq.(C.74) gives
We may call
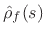 the reflectance of impedance
the reflectance of impedance 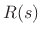 relative
to
relative
to 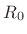 . For example, if a transmission line with characteristic
impedance
. For example, if a transmission line with characteristic
impedance 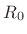 were terminated in a lumped impedance
were terminated in a lumped impedance 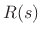 , the
reflection transfer function at the termination, as seen from the end
of the transmission line, would be
, the
reflection transfer function at the termination, as seen from the end
of the transmission line, would be
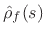 .
.
We are working with reflectance for force waves.
Using the elementary relations Eq.(C.73), i.e.,
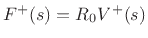 and
and
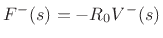 , we immediately obtain the corresponding
velocity-wave reflectance:
, we immediately obtain the corresponding
velocity-wave reflectance:
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() denote the driving-point impedance of an arbitrary
continuous-time LTI system. Then, by definition,
denote the driving-point impedance of an arbitrary
continuous-time LTI system. Then, by definition,
![]() where
where ![]() and
and ![]() denote the Laplace transforms
of the applied force and resulting velocity, respectively.
The wave variable decomposition in Eq.(C.74) gives
denote the Laplace transforms
of the applied force and resulting velocity, respectively.
The wave variable decomposition in Eq.(C.74) gives
![]() and
and
![]() , we immediately obtain the corresponding
velocity-wave reflectance:
, we immediately obtain the corresponding
velocity-wave reflectance: