Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Length  FIR Loop Filter Controlled by ``Brightness'' and ``Sustain''
FIR Loop Filter Controlled by ``Brightness'' and ``Sustain''
Another convenient parametrization of the second-order symmetric FIR
case is when the dc normalization is relaxed so that two degrees of
freedom are retained. It is then convenient to control them
as brightness 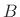 and sustain
and sustain 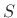 according to the
formulas
according to the
formulas
where  is the period in seconds (total loop delay),
is the period in seconds (total loop delay), 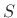 is the
desired sustain time in seconds, and
is the
desired sustain time in seconds, and 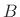 is the brightness parameter
in the interval
is the brightness parameter
in the interval ![$ [0,1]$](img1242.png) . The sustain parameter
. The sustain parameter 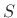 is defined here as
the time to decay by
is defined here as
the time to decay by 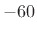 dB (or
dB (or
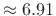 time-constants) when
brightness
time-constants) when
brightness 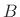 is maximum (
is maximum (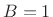 ) in which case the loop gain is
) in which case the loop gain is  at all frequencies, or
at all frequencies, or
 . As the brightness is
lowered, the dc gain remains fixed at
. As the brightness is
lowered, the dc gain remains fixed at  while higher frequencies
decay faster. At the minimum brightness, the gain at half the
sampling rate reaches zero, and the loop-filter amplitude-response
assumes the form
while higher frequencies
decay faster. At the minimum brightness, the gain at half the
sampling rate reaches zero, and the loop-filter amplitude-response
assumes the form
A Faust function implementing this FIR filter as the damping filter in
the Extended Karplus Strong (EKS) algorithm is described
in [456].
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() and sustain
and sustain ![]() according to the
formulas
according to the
formulas