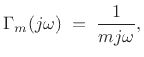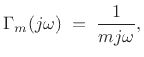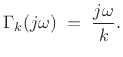Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Given force inputs and velocity outputs, the frequency response
of an ideal mass was given in Eq.(7.1.2) as
and the frequency response for a spring was given by Eq.(7.1.3) as
Thus, an ideal mass is an integrator and an ideal spring is a
differentiator. The modeling problem for masses and springs
can thus be posed as a problem in digital filter design given
the above desired frequency responses. More generally, the admittance
frequency response ``seen'' at the port of a general 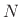 th-order LTI
system is, from Eq.(8.3),
th-order LTI
system is, from Eq.(8.3),
 |
(9.14) |
where we assume 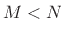 . Similarly, point-to-point
``trans-admittances'' can be defined as the velocity Laplace transform
at one point on the physical object divided by the driving-force
Laplace transform at some other point. There is also of course no
requirement to always use driving force and observed velocity as the
physical variables; velocity-to-force, force-to-force,
velocity-to-velocity, force-to-acceleration, etc., can all be used to
define transfer functions from one point to another in the system.
For simplicity, however, we will prefer admittance transfer functions
here.
. Similarly, point-to-point
``trans-admittances'' can be defined as the velocity Laplace transform
at one point on the physical object divided by the driving-force
Laplace transform at some other point. There is also of course no
requirement to always use driving force and observed velocity as the
physical variables; velocity-to-force, force-to-force,
velocity-to-velocity, force-to-acceleration, etc., can all be used to
define transfer functions from one point to another in the system.
For simplicity, however, we will prefer admittance transfer functions
here.
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]