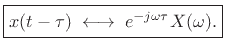Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Shift Theorem
The shift theorem for Fourier transforms states that
delaying a signal 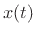 by
by 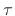 seconds multiplies its Fourier
transform by
seconds multiplies its Fourier
transform by
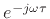 .
.
Proof:
Thus,
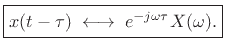 |
(B.12) |
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() by
by ![]() seconds multiplies its Fourier
transform by
seconds multiplies its Fourier
transform by
![]() .
.