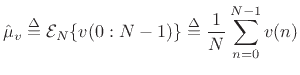Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Sample Mean
Definition:
The sample mean of a set of 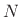 samples from a particular
realization of a stationary stochastic process
samples from a particular
realization of a stationary stochastic process  is defined
as the average of those samples:
is defined
as the average of those samples:
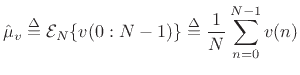 |
(C.17) |
For a stationary stochastic process  , the sample mean is
an unbiased estimator of the mean, i.e.,
, the sample mean is
an unbiased estimator of the mean, i.e.,
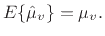 |
(C.18) |
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() samples from a particular
realization of a stationary stochastic process
samples from a particular
realization of a stationary stochastic process ![]() is defined
as the average of those samples:
is defined
as the average of those samples: