Probability Distribution

Definition: A probability distribution 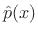$p(x)$ may be defined as a non-negative real function of all possible outcomes of some random event. The sum of the probabilities of all possible outcomes is defined as 1, and probabilities can never be negative.

Example: A coin toss has two outcomes, ``heads'' (H) or ``tails'' (T), which are equally likely if the coin is ``fair''. In this case, the probability distribution is

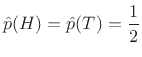$$p(H) = p(T) = \frac{1}{2}$$

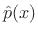where $p(x)$ denotes the probability of outcome 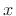$x$ . That is, the total ``probability mass'' is divided equally between the two possible outcomes heads or tails.