Two probabilistic events
![]() and
and ![]() are said to be
independent if the probability of
are said to be
independent if the probability of
![]() and
and ![]() occurring together equals the
product of the probabilities of
occurring together equals the
product of the probabilities of
![]() and
and ![]() individually, i.e.,
individually, i.e.,
| (C.2) |
Example:
Successive coin tosses are normally independent.
Therefore, the probability of getting heads twice in a row is
given by
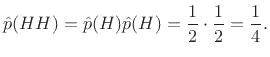 |
(C.3) |