Above, we used the Poisson Summation Formula to show that the constant-overlap-add of a window in the time domain is equivalent to the condition that the window transform have zero-crossings at all harmonics of the frame rate. In this section, we look briefly at the dual case: If the window transform is COLA in the frequency domain, what is the corresponding property of the window in the time domain? As one should expect, being COLA in the frequency domain corresponds to having specific uniform zero-crossings in the time domain.
Bandpass filters that sum to a constant provides an ideal basis for a graphic equalizer. In such a filter bank, when all the ``sliders'' of the equalizer are set to the same level, the filter bank reduces to no filtering at all, as desired.
Let ![]() denote the number of (complex) filters in our filter bank,
with pass-bands uniformly distributed around the unit circle. (We will
be using an FFT to implement such a filter bank.) Denote the
frequency response of the ``dc channel'' by
denote the number of (complex) filters in our filter bank,
with pass-bands uniformly distributed around the unit circle. (We will
be using an FFT to implement such a filter bank.) Denote the
frequency response of the ``dc channel'' by
![]() . Then the
constant overlap-add property of the
. Then the
constant overlap-add property of the ![]() -channel filter bank can be
expressed as
-channel filter bank can be
expressed as
| (9.35) |
 |
(9.36) |
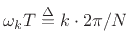 as usual. By the dual
of the Poisson summation formula, we have
as usual. By the dual
of the Poisson summation formula, we have
| (9.38) |
Thus, using the dual of the PSF, we have found that a good ![]() -channel
equalizer filter bank can be made using bandpass filters which have
zero-crossings at multiples of
-channel
equalizer filter bank can be made using bandpass filters which have
zero-crossings at multiples of ![]() samples, because that property
guarantees that the filter bank sums to a constant frequency response
when all channel gains are equal.
samples, because that property
guarantees that the filter bank sums to a constant frequency response
when all channel gains are equal.
The duality introduced in this section is the basis of the Filter-Bank Summation (FBS) interpretation of the short-time Fourier transform, and it is precisely the Fourier dual of the OverLap-Add (OLA) interpretation [9]. The FBS interpretation of the STFT is the subject of Chapter 9.