Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Perfect Reconstruction Cosine Modulated Filter Banks
By changing the phases 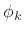 , the pseudo-QMF filter bank can yield
perfect reconstruction:
, the pseudo-QMF filter bank can yield
perfect reconstruction:
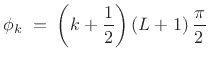 |
(12.101) |
where  is the length of the polyphase filter (
is the length of the polyphase filter (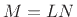 ).
).
If 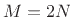 , then this is the
oddly stacked Princen-Bradley filter bank
and the analysis filters are related by cosine modulations of
the lowpass prototype:
, then this is the
oddly stacked Princen-Bradley filter bank
and the analysis filters are related by cosine modulations of
the lowpass prototype:
![$\displaystyle f_k(n) \eqsp h(n)\hbox{cos}\left[\left(n+\frac{N+1}{2}\right)\left(k+\frac{1}{2}\right)\frac{\pi}{N}\right],\quad k=0,\ldots,N-1$](img2254.png) |
(12.102) |
However, the length of the filters 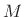 can be any even multiple of
can be any even multiple of 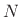 :
:
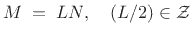 |
(12.103) |
The parameter  is called the overlapping factor. These
filter banks are also referred to as extended lapped
transforms, when
is called the overlapping factor. These
filter banks are also referred to as extended lapped
transforms, when 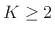 [159].
[159].
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() , the pseudo-QMF filter bank can yield
perfect reconstruction:
, the pseudo-QMF filter bank can yield
perfect reconstruction:
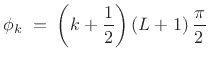
![]() , then this is the
oddly stacked Princen-Bradley filter bank
and the analysis filters are related by cosine modulations of
the lowpass prototype:
, then this is the
oddly stacked Princen-Bradley filter bank
and the analysis filters are related by cosine modulations of
the lowpass prototype:
![$\displaystyle f_k(n) \eqsp h(n)\hbox{cos}\left[\left(n+\frac{N+1}{2}\right)\left(k+\frac{1}{2}\right)\frac{\pi}{N}\right],\quad k=0,\ldots,N-1$](img2254.png)