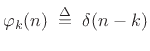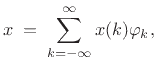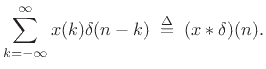Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
The natural basis for a discrete-time signal 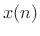 is the set
of shifted impulses:
is the set
of shifted impulses:
![$\displaystyle \varphi_k \isdefs [\ldots, 0,\underbrace{1}_{k^{\hbox{\tiny th}}},0,\ldots],$](img2282.png) |
(12.108) |
or,
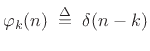 |
(12.109) |
for all integers 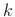 and
and 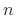 . The basis set is orthonormal since
. The basis set is orthonormal since
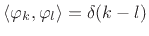 . The coefficient of projection of
. The coefficient of projection of 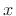 onto
onto 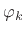 is given by
is given by
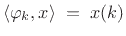 |
(12.110) |
so that the expansion of 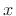 in terms of the natural basis is simply
in terms of the natural basis is simply
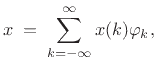 |
(12.111) |
i.e.,
This expansion was used in Book II [263] to derive the
impulse-response representation of an arbitrary linear, time-invariant
filter.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() is the set
of shifted impulses:
is the set
of shifted impulses:
![$\displaystyle \varphi_k \isdefs [\ldots, 0,\underbrace{1}_{k^{\hbox{\tiny th}}},0,\ldots],$](img2282.png)