Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Another way to add smoothness constraint is to add
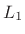 -norm of
the derivative to the objective:
-norm of
the derivative to the objective:
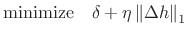 |
(4.82) |
Note that the
 norm is sensitive to all the derivatives,
not just the largest.
norm is sensitive to all the derivatives,
not just the largest.
We can formulate an LP problem by adding a vector of optimization
parameters  which bound derivatives:
which bound derivatives:
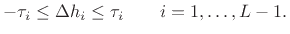 |
(4.83) |
In matrix form,
![$\displaystyle \left[\begin{array}{r} -\mathbf{D}\\ \mathbf{D}\end{array} \right]h-\left[\begin{array}{c} -\tau \\ -\tau \end{array} \right]\le 0.$](img635.png) |
(4.84) |
The objective function becomes
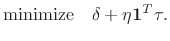 |
(4.85) |
See Fig.3.41 and Fig.3.42
for example results.
Figure:
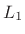 norm
of diff(h) added to the objective function (
norm
of diff(h) added to the objective function (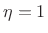 )
)
![\includegraphics[width=\twidth,height=6.5in]{eps/print_lone_chebwin_1}](img637.png) |
Figure:
Six times
the
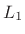 norm of diff(h) added to the objective function
(
norm of diff(h) added to the objective function
(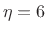 )
)
![\includegraphics[width=\twidth,height=6.5in]{eps/print_lone_chebwin_2}](img638.png) |
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() -norm of
the derivative to the objective:
-norm of
the derivative to the objective:
![]() which bound derivatives:
which bound derivatives:
![$\displaystyle \left[\begin{array}{r} -\mathbf{D}\\ \mathbf{D}\end{array} \right]h-\left[\begin{array}{c} -\tau \\ -\tau \end{array} \right]\le 0.$](img635.png)