Any ``reasonable'' probability density function (PDF) (§C.1.3)
has a Fourier transform that looks like
![]() near its tip. Iterating
near its tip. Iterating ![]() convolutions then corresponds to
convolutions then corresponds to
![]() , which becomes
[2]
, which becomes
[2]
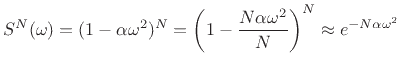 |
(D.27) |
Since the inverse Fourier transform of a Gaussian is another Gaussian
(§D.8), we can define a time-domain function ![]() as
being ``sufficiently regular'' when its Fourier transform approaches
as
being ``sufficiently regular'' when its Fourier transform approaches
![]() in a sufficiently small
neighborhood of
in a sufficiently small
neighborhood of ![]() . That is, the Fourier transform simply
needs a ``sufficiently smooth peak'' at
. That is, the Fourier transform simply
needs a ``sufficiently smooth peak'' at ![]() that can be
expanded into a convergent Taylor series. This obviously holds for
the DTFT of any discrete-time window function
that can be
expanded into a convergent Taylor series. This obviously holds for
the DTFT of any discrete-time window function ![]() (the subject of
Chapter 3), because the window transform
(the subject of
Chapter 3), because the window transform ![]() is a finite
sum of continuous cosines of the form
is a finite
sum of continuous cosines of the form
![]() in the
zero-phase case, and complex exponentials in the causal case, each of
which is differentiable any number of times in
in the
zero-phase case, and complex exponentials in the causal case, each of
which is differentiable any number of times in ![]() .
.