Getting Closer to Maximum Likelihood

In applications for which the fundamental frequency $F_0$ must be measured very accurately in a periodic signal, the estimate obtained by the above algorithm can be refined using a gradient search which matches a so-called harmonic comb to the magnitude spectrum of an interpolated FFT $X(\omega)$ :

$${\hat f}_0 \isdef \arg\max_{{\hat f}_0} \sum_{k=1}^K \log\left[\left\vert X(k{\hat f}_0)\right\vert+\epsilon\right]$$

$$= \arg\max_{{\hat f}_0} \prod_{k=1}^K \left[\left\vert X(k{\hat f}_0)\right\vert+\epsilon\right] \protect$$ (11.1)

where

$$\begin{eqnarray*} K &=& \mbox{number of peaks, and}\\ k &=& \mbox{harmonic number of $k$th peak}\\ \epsilon &=& \mbox{some small value on the order of the spectral magnitude}\\ & & \mbox{\lq\lq noise floor'' level} \end{eqnarray*}$$

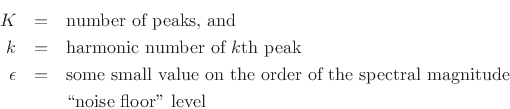
The purpose of $\epsilon>0$ is an insurance against multiplying the whole expression by zero due to a missing partial (e.g., due to a comb-filtering null). If $\epsilon=0$ in (10.1), it is advisable to omit indices $k$ for which $k{\hat f}_0$ is too close to a spectral null, since even one spectral null can push the product of peak amplitudes to a very small value. At the same time, the product should be penalized in some way to reflect the fact that it has fewer terms ( $\epsilon>0$ is one way to accomplish this).

As a practical matter, it is important to inspect the magnitude spectra of the data frame manually to ensure that a robust row of peaks is being matched by the harmonic comb. For example, it is typical to look at a display of the frame magnitude spectrum overlaid with vertical lines at the optimized harmonic-comb frequencies. This provides an effective picture of the $F_0$ estimate in which typical problems (such as octave errors) are readily seen.