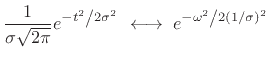Gaussian Window and Transform

The Gaussian ``bell curve'' is possibly the only smooth, nonzero function, known in closed form, that transforms to itself.^4.15

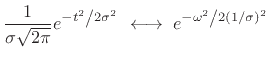$$\frac{1}{\sigma\sqrt{2\pi}}e^{-t^2 \left / 2\sigma^2\right.} \;\longleftrightarrow\; e^{-\omega^2 \left/ 2\left(1/\sigma\right)^2\right.}$$ (4.55)

It also achieves the minimum time-bandwidth product

$$\sigma_t\sigma_\omega = \sigma\times (1/\sigma) = 1$$ (4.56)

when ``width'' is defined as the square root of its second central moment. For even functions $w(t)$ ,

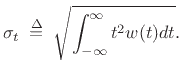$$\sigma_t \isdefs \sqrt{\int_{-\infty}^\infty t^2 w(t) dt}.$$ (4.57)

Since the true Gaussian function has infinite duration, in practice we must window it with some usual finite window, or truncate it.

Depalle [58] suggests using a triangular window raised to some power $\alpha$ for this purpose, which preserves the absence of side lobes for sufficiently large $\alpha$ . It also preserves non-negativity of the transform.