Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
It can be shown [44] that
 |
(4.58) |
where
![$ n\in[0,N-1]$](img572.png) is the time index, and
is the time index, and
![$ k\in[0,N-1]$](img100.png) is the
frequency index for a length
is the
frequency index for a length 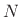 (even) normalized DFT
(DFT divided by
(even) normalized DFT
(DFT divided by 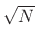 ). In other words, the Normalized DFT
(NDFT) of this particular sampled Gaussian pulse is exactly the
complex-conjugate of the same Gaussian pulse. (The proof is
nontrivial.)
). In other words, the Normalized DFT
(NDFT) of this particular sampled Gaussian pulse is exactly the
complex-conjugate of the same Gaussian pulse. (The proof is
nontrivial.)
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]