Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Differentiation Theorem
Let 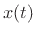 denote a function differentiable for all
denote a function differentiable for all 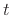 such that
such that
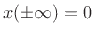 and the Fourier transforms (FT) of both
and the Fourier transforms (FT) of both 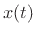 and
and
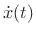 exist, where
exist, where
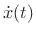 denotes the time derivative
of
denotes the time derivative
of 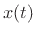 . Then we have
. Then we have
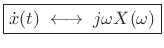 |
(B.4) |
where 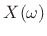 denotes the Fourier transform of
denotes the Fourier transform of 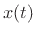 . In
operator notation:
. In
operator notation:
 |
(B.5) |
Proof:
This follows immediately from integration by parts:
since
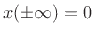 .
.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() denote a function differentiable for all
denote a function differentiable for all ![]() such that
such that
![]() and the Fourier transforms (FT) of both
and the Fourier transforms (FT) of both ![]() and
and
![]() exist, where
exist, where
![]() denotes the time derivative
of
denotes the time derivative
of ![]() . Then we have
. Then we have
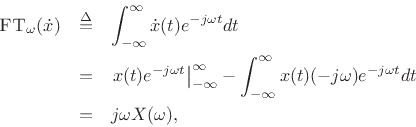
![]() .
.