Let ![]() be continuous on a real interval
be continuous on a real interval ![]() containing
containing ![]() (and
(and ![]() ),
and let
),
and let
![]() exist at
exist at ![]() and
and
![]() be continuous for
all
be continuous for
all ![]() . Then we have the following Taylor series expansion:
. Then we have the following Taylor series expansion:
![\begin{eqnarray*}
f(x) = f(x_0) &+& \frac{1}{1}f^\prime(x_0)(x-x_0) \\ [10pt]
&+& \frac{1}{1\cdot 2}f^{\prime\prime}(x_0)(x-x_0)^2 \\ [10pt]
&+& \frac{1}{1\cdot 2\cdot 3}f^{\prime\prime\prime}(x_0)(x-x_0)^3\\ [10pt]
&+& \cdots\\ [10pt]
&+& \frac{1}{n!}f^{(n+1)}(x_0)(x-x_0)^n\\ [10pt]
&+& R_{n+1}(x)
\end{eqnarray*}](img1867.png)
where
![]() is called the remainder term. Then Taylor's
theorem [66, pp. 95-96] provides that there exists some
is called the remainder term. Then Taylor's
theorem [66, pp. 95-96] provides that there exists some ![]() between
between ![]() and
and ![]() such that
such that
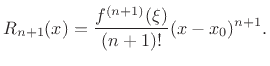
In particular, if
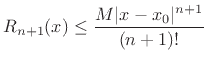
which is normally small when
When ![]() , the Taylor series reduces to what is called a Maclaurin
series [59, p. 96].
, the Taylor series reduces to what is called a Maclaurin
series [59, p. 96].