Downsampling Theorem (Aliasing Theorem)

Theorem: For all $x\in\mathbb{C}^N$ ,

$$\zbox {\hbox{\sc Downsample}_L(x) \;\longleftrightarrow\;\frac{1}{L}\hbox{\sc Alias}_L(X).}$$

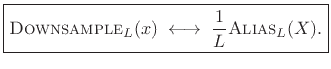
Proof: Let $k^\prime \in[0,M-1]$ denote the frequency index in the aliased spectrum, and let $Y(k^\prime )\isdef \hbox{\sc Alias}_{L,k^\prime }(X)$ . Then $Y$ is length $M=N/L$ , where $L$ is the downsampling factor. We have

$$\begin{eqnarray*} Y(k^\prime ) &\isdef & \hbox{\sc Alias}_{L,k^\prime }(X) \isdef \sum_{l=0}^{L-1}X(k^\prime +lM), \quad k^\prime =0,1,2,\ldots,M-1 \\ [5pt] &\isdef & \sum_{l=0}^{L-1}\sum_{n=0}^{N-1}x(n) e^{-j2\pi(k^\prime +lM)n/N} \\ [5pt] &\isdef & \sum_{n=0}^{N-1}x(n) e^{-j2\pi k^\prime n/N} \sum_{l=0}^{L-1}e^{-j2\pi l n M/N}. \end{eqnarray*}$$

Since $M/N=1/L$ , the sum over $l$ becomes

$$\sum_{l=0}^{L-1}\left[e^{-j2\pi n/L}\right]^l = \frac{1-e^{-j2\pi n}}{1-e^{-j2\pi n/L}} = \left\{\begin{array}{ll} L, & n=0 \left(\mbox{mod}\;L\right) \\ [5pt] 0, & n\neq 0 \left(\mbox{mod}\;L\right) \\ \end{array} \right.$$

using the closed form expression for a geometric series derived in §6.1. We see that the sum over $l$ effectively samples $x$ every $L$ samples. This can be expressed in the previous formula by defining $m\isdeftext n/L$ which ranges only over the nonzero samples:

$$\begin{eqnarray*} \hbox{\sc Alias}_{L,k^\prime }(X) &=& \sum_{n=0}^{N-1}x(n) e^{-j2\pi k^\prime n/N} \sum_{l=0}^{L-1}e^{-j2\pi l n /L} \\ &=& L\sum_{m=0}^{N/L-1} x(mL) e^{-j2\pi k^\prime (m L) /N}\qquad(m\isdef n/L) \\ &\isdef & L\sum_{m=0}^{M-1}x(mL) e^{-j2\pi k^\prime m /M}\\ &\isdef & L\sum_{m=0}^{M-1}\hbox{\sc Downsample}_{L,m}(x) e^{-j2\pi k^\prime m /M} \\ &\isdef & L\cdot \hbox{\sc DFT}_{k^\prime }(\hbox{\sc Downsample}_L(x)) \end{eqnarray*}$$

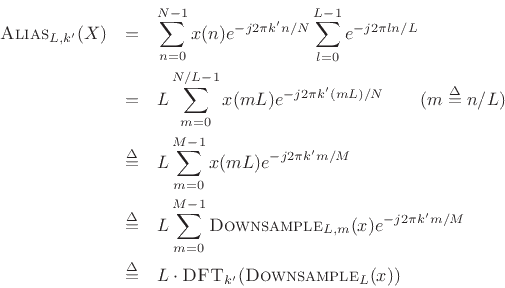
Since the above derivation also works in reverse, the theorem is proved.

An illustration of aliasing in the frequency domain is shown in Fig.7.12.