Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Lagrange Interpolation
Lagrange interpolation is a well known, classical technique for
interpolation [194]. It is also called Waring-Lagrange
interpolation, since Waring actually published it 16 years before
Lagrange [312, p. 323]. More generically, the term
polynomial interpolation normally refers to Lagrange interpolation.
In the first-order case, it reduces to linear interpolation.
Given a set of 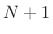 known samples
known samples 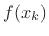 ,
,
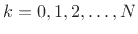 , the
problem is to find the unique order
, the
problem is to find the unique order 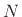 polynomial
polynomial 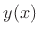 which
interpolates the samples.5.2The solution can be expressed as a linear combination of elementary
which
interpolates the samples.5.2The solution can be expressed as a linear combination of elementary
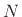 th order polynomials:
th order polynomials:
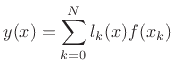 |
(5.6) |
where
From the numerator of the above definition, we see that 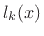 is an
order
is an
order 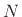 polynomial having zeros at all of the samples except the
polynomial having zeros at all of the samples except the
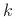 th. The denominator is simply the constant which normalizes
to give
th. The denominator is simply the constant which normalizes
to give
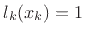 . Thus, we have
. Thus, we have
The polynomial 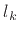 can be interpreted as the
can be interpreted as the 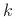 th basis polynomial
for constructing a polynomial interpolation of order
th basis polynomial
for constructing a polynomial interpolation of order 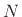 over the
over the
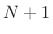 sample points
sample points 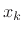 . It is an order
. It is an order 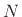 polynomial having zeros
at all of the samples except the
polynomial having zeros
at all of the samples except the 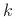 th, where it is 1. An example of
a set of eight basis functions
th, where it is 1. An example of
a set of eight basis functions 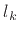 for randomly selected
interpolation points
for randomly selected
interpolation points 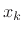 is shown in Fig.4.10.
is shown in Fig.4.10.
Figure 4.10:
Example Lagrange basis functions
in the eighth-order case for randomly selected interpolation points
(marked by dotted lines). The unit-amplitude points are marked by
dashed lines.
![\includegraphics[width=\twidth]{eps/lagrangebases}](img1014.png) |
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() known samples
known samples ![]() ,
,
![]() , the
problem is to find the unique order
, the
problem is to find the unique order ![]() polynomial
polynomial ![]() which
interpolates the samples.5.2The solution can be expressed as a linear combination of elementary
which
interpolates the samples.5.2The solution can be expressed as a linear combination of elementary
![]() th order polynomials:
th order polynomials:
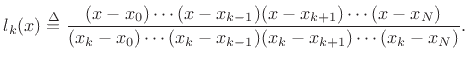
![$\displaystyle l_k(x_j) = \delta_{kj} \isdef \left\{\begin{array}{ll}
1, & j=k, \\ [5pt]
0, & j\neq k. \\
\end{array} \right.
$](img1011.png)
![\includegraphics[width=\twidth]{eps/lagrangebases}](img1014.png)