Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
A large class of well posed PDEs is given by [43]
 |
(G.30) |
Thus, to the ideal string wave equation Eq. (G.1) we add any number
of even-order partial derivatives in 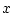 , plus any number of mixed
odd-order partial derivatives in
, plus any number of mixed
odd-order partial derivatives in 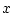 and
and 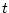 , where differentiation
with respect to
, where differentiation
with respect to 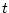 occurs only once. Because every member of this
class of PDEs is only second-order in time, it is guaranteed to be
well posed, as shown in §L.2.2.
occurs only once. Because every member of this
class of PDEs is only second-order in time, it is guaranteed to be
well posed, as shown in §L.2.2.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite and copy this work]
