Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
State Conversions
In §G.3.5, an arbitrary string state was converted to
traveling displacement-wave components to show that the traveling-wave
representation is complete, i.e., that any physical string state can be
expressed as a pair of traveling-wave components. In this section, we
revisit this topic using force and velocity waves.
By definition of the traveling-wave decomposition, we have
Using Eq. (G.45), we can eliminate
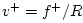 and
and
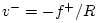 ,
giving, in matrix form,
,
giving, in matrix form,
Thus, the string state (in terms of force and velocity) is expressed
as a linear transformation of the traveling force-wave components. Using
the Ohm's law relations to eliminate instead
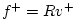 and
and
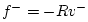 ,
we obtain
To convert an arbitrary initial string state
,
we obtain
To convert an arbitrary initial string state 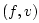 to either a
traveling force-wave or velocity-wave simulation, we simply must be
able to invert the appropriate two-by-two matrix above. That
is, the matrix must be nonsingular. Requiring both
determinants to be nonzero yields the condition
That is, the wave impedance must be a positive, finite number. This
restriction makes good physical sense because one cannot propagate a
finite-energy wave in either a zero or infinite wave impedance.
to either a
traveling force-wave or velocity-wave simulation, we simply must be
able to invert the appropriate two-by-two matrix above. That
is, the matrix must be nonsingular. Requiring both
determinants to be nonzero yields the condition
That is, the wave impedance must be a positive, finite number. This
restriction makes good physical sense because one cannot propagate a
finite-energy wave in either a zero or infinite wave impedance.
Carrying out the inversion to obtain force waves
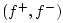 from
from
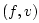 yields
yields
Similarly, velocity waves
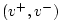 are prepared from
are prepared from 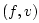 according to
according to
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite and copy this work]
![]() and
and
![]() ,
giving, in matrix form,
,
giving, in matrix form,
![]() from
from
![]() yields
yields
![$\displaystyle \left[\begin{array}{c} f^{{+}} \\ [2pt] f^{{-}} \end{array}\right...
...ft[\begin{array}{c} \frac{f+Rv}{2} \\ [2pt] \frac{f-Rv}{2} \end{array}\right].
$](img1818.png)
![$\displaystyle \left[\begin{array}{c} v^{+} \\ [2pt] v^{-} \end{array}\right] = ...
...[\begin{array}{c} \frac{v+f/R}{2} \\ [2pt] \frac{v-f/R}{2} \end{array}\right].
$](img1820.png)