More General Allpass Filters

We have so far seen two types of allpass filters:

• The series combination of feedback and feedforward comb-filters is allpass when their delay lines are the same length and their feedback and feedforward coefficents are the same. An example is shown in Fig. 1.24.
• Any delay element in an allpass filter can be replaced by an allpass filter to obtain a new (typically higher order) allpass filter. The special case of nested first-order allpass filters yielded the lattice digital filter structure of Fig. 1.26.

We now discuss allpass filters more generally in the SISO case. (See Appendix D of [426] for the MIMO case.)

Definition: A linear, time-invariant filter $H(z)$ is said to be lossless if it preserves signal energy for every input signal. That is, if the input signal is $x(n)$, and the output signal is $y(n) = (h\ast x)(n)$, we must have

$$\sum_{n=-\infty}^{\infty} \left\vert y(n)\right\vert^2 = \sum_{n=-\infty}^{\infty} \left\vert x(n)\right\vert^2.$$

In terms of the $L2$ signal norm $\left\Vert\,\,\cdot\,\,\right\Vert _2$, this can be expressed more succinctly as

$$\left\Vert\,y\,\right\Vert _2^2 = \left\Vert\,x\,\right\Vert _2^2.$$

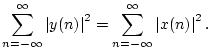
Notice that only stable filters can be lossless since, otherwise, $\left\Vert\,y\,\right\Vert$ is generally infinite, even when $\left\Vert\,x\,\right\Vert$ is finite. We further assume all filters are causal^2.9 for simplicity. It is straightforward to show the following:

It can be shown [426, Appendix D] that stable, linear, time-invariant (LTI) filter transfer function $H(z)$ is lossless if and only if

$$\left\vert H(e^{j\omega})\right\vert = 1, \quad \forall \omega.$$

That is, the frequency response must have magnitude 1 everywhere over the unit circle in the complex $z$ plane.

Thus, ``lossless'' and ``unity-gain allpass'' are synonymous. For an allpass filter with gain $g$ at each frequency, the energy gain of the filter is $g^2$ for every input signal $x$. Since we can describe such a filter as an allpass times a constant gain, the term ``allpass'' will refer here to the case $g=1$.