From Newton's second law,
![]() (introduced in
Eq. (E.1)), we can derive the formula for the kinetic energy of a mass
given its speed
(introduced in
Eq. (E.1)), we can derive the formula for the kinetic energy of a mass
given its speed
![]() . Let
. Let ![]() denote a small (infinitesimal)
displacement of the mass in the
denote a small (infinitesimal)
displacement of the mass in the ![]() direction. Then we have, using
the calculus of differentials,
direction. Then we have, using
the calculus of differentials,
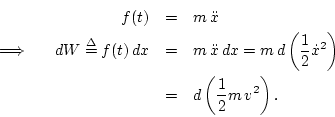
Thus, by Newton's second law, a differential of work ![]() applied to a
mass
applied to a
mass ![]() by force
by force ![]() through distance
through distance ![]() boosts the kinetic energy
of the mass by
boosts the kinetic energy
of the mass by
![]() . Therefore, we must have
. Therefore, we must have
The quantity ![]() is classically called the virtual work
associated with force
is classically called the virtual work
associated with force ![]() , and
, and ![]() a virtual displacement
[521].
a virtual displacement
[521].