Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Let 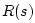 denote a general impedance. Then the wave variable
decomposition in (J.7) gives
denote a general impedance. Then the wave variable
decomposition in (J.7) gives
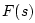 |
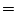 |
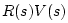 |
(J.13) |
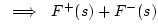 |
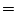 |
![$\displaystyle R(s) \left[V^{+}(s) + V^{-}(s)\right]$](img2593.png) |
(J.14) |
| |
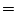 |
![$\displaystyle R(s) \left[\frac{F^{+}(s) - F^{-}(s)}{R_0}\right]$](img2594.png) |
(J.15) |
![$\displaystyle \,\,\implies\,\,F^{-}(s) \left[\frac{R(s)}{R_0}+1\right]$](img2595.png) |
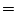 |
![$\displaystyle F^{+}(s) \left[\frac{R(s)}{R_0}-1\right]$](img2596.png) |
(J.16) |
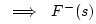 |
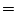 |
![$\displaystyle F^{+}(s) \left[\frac{R(s)-R_0}{R(s)+R_0}\right]$](img2598.png) |
(J.17) |
| |
 |
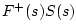 |
(J.18) |
Formally,  is the reflectance of impedance
is the reflectance of impedance 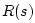 relative
to
relative
to 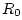 . For example, if a transmission line with characteristic
impedance
. For example, if a transmission line with characteristic
impedance 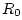 were terminated in a lumped impedance
were terminated in a lumped impedance 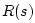 , the
reflection transfer function at the termination would be
, the
reflection transfer function at the termination would be 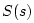 . The
interpretation of
. The
interpretation of 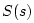 as a reflectance is shown
as a wave flow diagram in
Fig. J.17c.
as a reflectance is shown
as a wave flow diagram in
Fig. J.17c.
Figure J.17:
Three different types
of diagram for a basic impedance relation:
a) Impedance diagram.
b) System block diagram.
c) Wave flow diagram.
![\includegraphics[width=\twidth]{eps/lreflectance}](img2601.png) |
We are working with reflectance for force waves.
Using the elementary relations (J.7), i.e.,
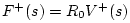 and
and
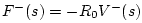 , we immediately obtain the corresponding
velocity-wave reflectance
, we immediately obtain the corresponding
velocity-wave reflectance
Thus, velocity reflectance is simply the negative of force reflectance.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite and copy this work]
![]() denote a general impedance. Then the wave variable
decomposition in (J.7) gives
denote a general impedance. Then the wave variable
decomposition in (J.7) gives
![\includegraphics[width=\twidth]{eps/lreflectance}](img2601.png)
![]() and
and
![]() , we immediately obtain the corresponding
velocity-wave reflectance
, we immediately obtain the corresponding
velocity-wave reflectance