Air Absorption

This section provides some further details regarding acoustic air absorption [298]. For a plane wave, the decline of acoustic intensity as a function of propagation distance 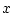$x$ is given by

$$I(x) = I_0 e^{-x/\xi},$$

where

$$\begin{eqnarray*} I_0 &=& \hbox{intensity at the source (\sref {intensity} def... ...n frequency, temperature, humidity}\\ & & \hbox{and pressure).} \end{eqnarray*}$$

Tables E.1 and E.2 (adapted from [294]) give some typical values for air.

Table E.1: Attenuation constant 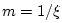$m = 1/\xi$ (in inverse meters) at 20 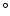${}^{\circ }$C and standard atmospheric pressure

Relative	Frequency in Hz
Humidity	1000	2000	3000	4000
40	0.0013	0.0037	0.0069	0.0242
50	0.0013	0.0027	0.0060	0.0207
60	0.0013	0.0027	0.0055	0.0169
70	0.0013	0.0027	0.0050	0.0145

Table E.2: Attenuation in dB per kilometer at 20 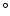${}^{\circ }$C and standard atmospheric pressure.

Relative	Frequency in Hz
Humidity	1000	2000	3000	4000
40	5.6	16	30	105
50	5.6	12	26	90
60	5.6	12	24	73
70	5.6	12	22	63