One-Multiply Scattering Junctions

By factoring out 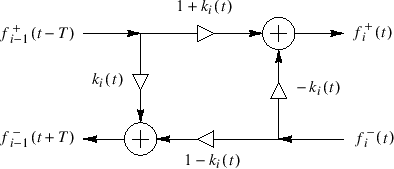$k_i(t)$ in each equation of (C.60), we can write

$$f^{{+}}_i(t) = f^{{+}}_{i-1}(t-T) + f_{{\Delta}}(t)$$

$$f^{{-}}_{i-1}(t+T) = f^{{-}}_i(t) + f_{{\Delta}}(t)$$ (C.62)

where

$$f_{{\Delta}}(t) \isdef k_i(t)\left[f^{{+}}_{i-1}(t-T) - f^{{-}}_i(t) \right]$$ (C.63)

Thus, only one multiplication is actually necessary to compute the transmitted and reflected waves from the incoming waves in the Kelly-Lochbaum junction. This computation is shown in Fig.C.21, and it is known as the one-multiply scattering junction [299].

Figure C.21: The one-multiply scattering junction.

Another one-multiply form is obtained by organizing (C.60) as

$$f^{{+}}_i(t) = f^{{-}}_i(t) + \alpha_i(t)\tilde{f_d}(t)$$

$$f^{{-}}_{i-1}(t+T) = f^{{+}}_i(t) - \tilde{f_d}(t)$$ (C.64)

where

$$\alpha_i(t) \isdef 1+k_i(t)$$

$$\tilde{f_d}(t) \isdef f^{{+}}_{i-1}(t-T) - f^{{-}}_i(t).$$ (C.65)

As in the previous case, only one multiplication and three additions are required per junction. This one-multiply form generalizes more readily to junctions of more than two waveguides, as we'll see in a later section.

A scattering junction well known in the LPC speech literature but not described here is the so-called two-multiply junction [299] (requiring also two additions). This omission is because the two-multiply junction is not valid as a general, local, physical modeling building block. Its derivation is tied to the reflectively terminated, cascade waveguide chain. In cases where it applies, however, it can be the implementation of choice; for example, in DSP chips having a fast multiply-add instruction, it may be possible to implement the inner loop of the two-multiply, two-add scattering junction using only two instructions.