The mass moment of inertia ![]() (or simply moment of
inertia), plays the role of mass in rotational dynamics, as
we saw in
Eq.(B.7) above.
(or simply moment of
inertia), plays the role of mass in rotational dynamics, as
we saw in
Eq.(B.7) above.
The mass moment of inertia of a rigid body, relative to a given axis of rotation, is given by a weighted sum over its mass, with each mass-point weighted by the square of its distance from the rotation axis. Compare this with the center of mass (§B.4.1) in which each mass-point is weighted by its vector location in space (and divided by the total mass).
Equation (B.8) above gives the moment of inertia for a single point-mass
![]() rotating a distance
rotating a distance ![]() from the axis to be
from the axis to be ![]() . Therefore,
for a rigid collection of point-masses
. Therefore,
for a rigid collection of point-masses ![]() ,
,
![]() ,B.14 the
moment of inertia about a given axis of rotation is obtained by adding
the component moments of inertia:
,B.14 the
moment of inertia about a given axis of rotation is obtained by adding
the component moments of inertia:
For a continuous mass distribution, the moment of inertia is given by integrating the contribution of each differential mass element:
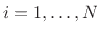 |
(B.10) |
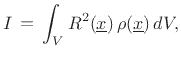
where