Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
As derived in §4.2.14, Lagrange fractional-delay filters are
maximally flat in the frequency domain at dc. That is,
where  is the interpolation error expressed in the frequency domain:
is the interpolation error expressed in the frequency domain:
where 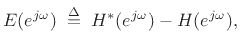 and
and 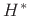 are defined in §4.2.2 above. This is
the same optimality criterion used for the power response of (recursive)
Butterworth filters in classical analog filter design
[346,452]. It can also be formulated in terms of
``Pade approximation'' [376,377]. To summarize, the basic idea
of maximally flat filter design is to match exactly as many leading
terms as possible in the Taylor series expansion of the desired
frequency response. Equivalently, we zero the maximum number of leading
terms in the Taylor expansion of the frequency-response error.
are defined in §4.2.2 above. This is
the same optimality criterion used for the power response of (recursive)
Butterworth filters in classical analog filter design
[346,452]. It can also be formulated in terms of
``Pade approximation'' [376,377]. To summarize, the basic idea
of maximally flat filter design is to match exactly as many leading
terms as possible in the Taylor series expansion of the desired
frequency response. Equivalently, we zero the maximum number of leading
terms in the Taylor expansion of the frequency-response error.
Figure 4.11 compares Lagrange and optimal Chebyshev fractional-delay
filter frequency responses. Optimality in the Chebyshev
sense means minimizing the worst-case
error over a given frequency band (in this case,
![$ \vert\omega\vert\in
[0,0.8\pi]$](img1032.png) ). While Chebyshev optimality is often the most desirable
choice, we do not have closed-form formulas for such solutions, so they
must be laboriously pre-calculated, tabulated, and interpolated to
produce variable-delay filtering [361].
). While Chebyshev optimality is often the most desirable
choice, we do not have closed-form formulas for such solutions, so they
must be laboriously pre-calculated, tabulated, and interpolated to
produce variable-delay filtering [361].
Figure 4.11:
Comparison of Lagrange and Optimal Chebyshev Fractional-Delay Filter Frequency Responses
![\includegraphics[width=3.5in]{eps/lag}](img1033.png) |
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
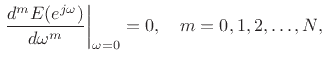
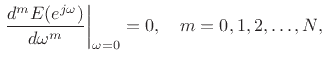
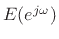
![]() ). While Chebyshev optimality is often the most desirable
choice, we do not have closed-form formulas for such solutions, so they
must be laboriously pre-calculated, tabulated, and interpolated to
produce variable-delay filtering [361].
). While Chebyshev optimality is often the most desirable
choice, we do not have closed-form formulas for such solutions, so they
must be laboriously pre-calculated, tabulated, and interpolated to
produce variable-delay filtering [361].
![\includegraphics[width=3.5in]{eps/lag}](img1033.png)