Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
- Comparing digital and analog frequency formulas.
This first exercise verifies that the elementary ``tank circuit''
always resonates at exactly the frequency it should, according to the
bilinear transform frequency mapping
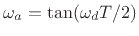 , where
, where 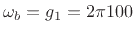 denotes ``analog frequency'' and
denotes ``analog frequency'' and 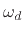 denotes ``digital frequency''.
denotes ``digital frequency''.
- Find the poles of Fig.F.37 in terms of
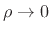 .
.
- Show that the resonance frequency is given by
where 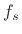 denotes the sampling rate.
denotes the sampling rate.
- Recall that the mass-spring oscillator resonates at
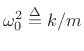 . Relate these two resonance frequency formulas
via the analog-digital frequency map
. Relate these two resonance frequency formulas
via the analog-digital frequency map
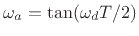 .
.
- Show that the trig identity you discovered in this way is true.
I.e., show that
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
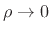 .
.

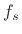 denotes the sampling rate.
denotes the sampling rate.
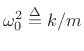 . Relate these two resonance frequency formulas
via the analog-digital frequency map
. Relate these two resonance frequency formulas
via the analog-digital frequency map
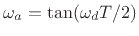 .
.
![$\displaystyle f_s \arccos\left[\frac{k-m}{k+m}\right] =
2f_s \arctan\left[\sqrt{\frac{m}{k}}\right].
$](img5159.png)