If the change in ![]() or
or ![]() is deemed to be ``internal'', that is,
involving no external interactions, the appropriate accompanying
change in the internal state variables is that which conserves
energy. For the mass and its velocity, for example, we must have
is deemed to be ``internal'', that is,
involving no external interactions, the appropriate accompanying
change in the internal state variables is that which conserves
energy. For the mass and its velocity, for example, we must have
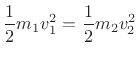
where
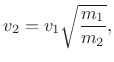
since this holds the kinetic energy of the mass constant. Note that the momentum of the mass is changed, however, since
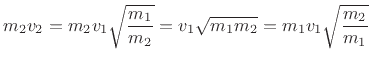
If the spring constant ![]() is to change from
is to change from ![]() to
to ![]() , the
instantaneous spring displacement
, the
instantaneous spring displacement ![]() must satisfy
must satisfy

In a velocity-wave simulation, displacement is the integral of velocity. Therefore, the energy-conserving velocity correction is impulsive in this case.