Suppose now that the body-fixed frame is rotating in the space-fixed
frame with angular velocity
![]() . Then the total torque on the rigid
body becomes [272]
. Then the total torque on the rigid
body becomes [272]
If the body-fixed frame is aligned with the principal axes of rotation (§B.4.16), then the mass moment of inertia tensor is diagonal, say
![$\displaystyle \underline{L}\eqsp \left[\begin{array}{c} I_1\omega_1 \\ [2pt] I_2\omega_2 \\ [2pt] I_3\omega_3\end{array}\right]
$](img2973.png)
so that the term
![\begin{eqnarray*}
\underline{\omega}\times\underline{L}&\!=\!&
\left\vert \begin{array}{ccc}
\underline{e}_1 & \underline{e}_2 & \underline{e}_3\\ [2pt]
\underline{\omega}_1 & \underline{\omega}_2 & \underline{\omega}_3\\ [2pt]
I_1\omega_1 & I_2\omega_2 & I_3\omega_3
\end{array}\right\vert\\ [5pt]
&\!=\!& \mbox{\small$(\underline{\omega}_2 I_3\omega_3 - I_2\omega_2 \underline{\omega}_3)\underline{e}_1 + (\underline{\omega}_3I_1\omega_1 - I_3\omega_3\underline{\omega}_1) \underline{e}_2 + (\underline{\omega}_1I_2\omega_2- I_1\omega_1\underline{\omega}_2) \underline{e}_3$}\\ [5pt]
&\!=\!&
(I_3-I_2)\omega_2\omega_3\,\underline{e}_1 +
(I_1-I_3)\omega_3\omega_1\,\underline{e}_2 +
(I_2-I_1)\omega_1\omega_2\,\underline{e}_3.
\end{eqnarray*}](img2975.png)
Substituting this result into Eq.(B.30), we obtain the following equations of angular motion for an object rotating in the body-fixed frame defined by its three principal axes of rotation:
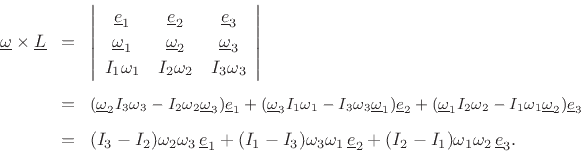
These are call Euler's
equations:B.29Since these equations are in the body-fixed frame, ![]() is the mass
moment of inertia about principal axis
is the mass
moment of inertia about principal axis ![]() , and
, and ![]() is the
angular velocity about principal axis
is the
angular velocity about principal axis ![]() .
.