Digitizing Bridge Reflectance

Converting continuous-time transfer functions such as $\hat{\rho}_b(s)$ and $\hat{\tau}_b(s)$ to the digital domain is analogous to converting an analog electrical filter to a corresponding digital filter--a problem which has been well studied [346]. For this task, the bilinear transform (§7.3.2) is a good choice. In addition to preserving order and being free of aliasing, the bilinear transform preserves the positive-real property of passive impedances (§C.11.2).

Digitizing $\hat{\rho}_b(s)$ via the bilinear transform (§7.3.2) transform gives

$$\hat{\rho}_b^d(z) \isdefs \hat{\rho}_b\left(c\frac{1-z^{-1}}{1+z^{-1}}\right)$$

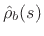
which is a second-order digital filter having gain less than one at all frequencies--i.e., it is a Schur filter that becomes an allpass as the damping $\mu$ approaches zero. The choice of bilinear-transform constant $c=1/\tan(\omega_0T/2)$ maps the peak-frequency $\omega_0$ without error (see Problem 4).