Diffuse Reflections in the Waveguide Mesh

In [419], Manfred Schroeder proposed the design of a diffuse reflector based on a quadratic residue sequence. A quadratic residue sequence $a_p(n)$ corresponding to a prime number $p$ is the sequence $n^2$ mod $p$ , for all integers $n$ . The sequence is periodic with period $p$ , so it is determined by $a_p(n)$ for $n=0,1,2,\ldots,p-1$ (i.e., one period of the infinite sequence).

For example, when $p=7$ , the first period of the quadratic residue sequence is given by

$$\begin{eqnarray*} a_7 &=& [0^2,1^2,2^2,3^2,4^2,5^2,6^2] \quad (\mbox{mod }7)\\ &=& [0, 1, 4, 2, 2, 4, 1] \end{eqnarray*}$$

An amazing property of these sequences is that their Fourier transforms have precisely constant magnitudes. That is, the sequence

$$c_p(n) \isdef e^{j\frac{2\pi}{p} a_p(n)}$$

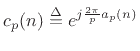
has a DFT with exactly constant magnitude:^C.14

$$\vert C_p(\omega_k)\vert \isdef \vert\dft _k(c_p)\vert \isdef \left\vert\sum_{n=0}^{p-1} c_p(n) e^{-j2\pi nk/p}\right\vert = \sqrt{p}, \quad \forall k\in[0,p-1]$$

This property can be used to give highly diffuse reflections for incident plane waves.

Figure C.37 presents a simple matlab script which demonstrates the constant-magnitude Fourier property for all odd integers from 1 to 99.

Figure C.37: Matlab script for demonstrating the Fourier property of an odd-length quadratic residue sequence.

 

function [c] = qrsfp(Ns)
%QRSFP Quadratic Residue Sequence Fourier Property demo
  if (nargin<1)
     Ns = 1:2:99; % Test all odd integers from 1 to 99
  end
  for N=Ns
    a = mod([0:N-1].^2,N);
    c = zeros(N-1,N);
    CM = zeros(N-1,N);
    c = exp(j*2*pi*a/N);
    CM = abs(fft(c))*sqrt(1/N);
    if (abs(max(CM)-1)>1E-10) || (abs(min(CM)-1)>1E-10)
       warn(sprintf("Failure for N=%d",N));
    end
  end
  r = exp(2i*pi*[0:100]/100); % a circle
  plot(real(r), imag(r),"k"); hold on;
  plot(c,"-*k"); % plot sequence in complex plane
end

Quadratic residue diffusers have been applied as boundaries of a 2D digital waveguide mesh in [281]. An article reviewing the history of room acoustic diffusers may be found in [94].^C.15