Consistency

A finite-difference scheme is said to be consistent with the original partial differential equation if, given any sufficiently differentiable function $y(t,x)$ , the differential equation operating on $y(t,x)$ approaches the value of the finite difference equation operating on $y(nT,mX)$ , as $T$ and $X$ approach zero.

Thus, in the ideal string example, to show the consistency of Eq.(D.3) we must show that

$$\left(\frac{\partial^2}{\partial x^2} - \frac{1}{c^2} \frac{\partial^2}{\partial t^2} \right)y(t,x) = \lim_{T,X\to0} \left[ (\delta_x + \delta_x^{-1}) - (\delta_t + \delta_t^{-1}) \right] y_{n,m}$$

for all $y(t,x)$ which are second-order differentiable with respect to $t$ and $x$ . On the right-hand side, we have introduced the following shift operator notation:

$$\delta_t^k y_{n,m} \isdef y_{n-k,m}$$

$$\delta_x^k y_{n,m} \isdef y_{n,m-k} \protect$$ (D.4)

In particular, we have

$$\begin{eqnarray*} \delta_t y_{n,m}&\isdef & y_{n-1,m}\\ \delta_t^{-1} y_{n,m}&\isdef & y_{n+1,m}\\ \delta_x y_{n,m}&\isdef & y_{n,m-1}\\ \delta_x^{-1} y_{n,m}&\isdef & y_{n,m+1}. \end{eqnarray*}$$

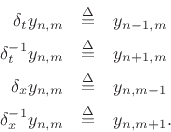
In taking the limit as $T$ and $X$ approach zero, we must maintain the relationship $X=cT$ , and we must scale the FDS by $1/X^2$ in order to achieve an exact result:

$$\begin{eqnarray*} \lefteqn{\lim_{T,X\to0} \frac{1}{X^2} \left[ (\delta_x + \delta_x^{-1}) - (\delta_t + \delta_t^{-1}) \right] y_{n,m}} \qquad\qquad& &\\ &=& \lim_{T,X\to0} \left[ \frac{\delta_x + 2 + \delta_x^{-1}}{X^2} - \frac{\delta_t + 2 + \delta_t^{-1}}{c^2T^2} \right] y_{n,m}\\ &\isdef & \left(\frac{\partial^2}{\partial x^2} - \frac{1}{c^2} \frac{\partial^2}{\partial t^2} \right)y(t,x) \end{eqnarray*}$$

as required. Thus, the FDS is consistent. See, e.g., [484] for more examples.

In summary, consistency of a finite-difference scheme means that, in the limit as the sampling intervals approach zero, the original PDE is obtained from the FDS.