The Bow-String Scattering Junction

The theory of bow-string interaction is described in [95,151,246,310,311]. The basic operation of the bow is to reconcile the nonlinear bow-string friction curve $R_b(v_d)$ with the string wave impedance $R_s$ :

$$\begin{eqnarray*} \mbox{Applied Force} &=& \mbox{Bow-String Friction Curve} \times \mbox{Differential Velocity} \\ \mbox{Reaction Force} &=& \mbox{String Wave Impedance} \times \mbox{Velocity Change} \end{eqnarray*}$$

or, equating these equal and opposite forces, we obtain

$$R_b(v_{\Delta})\times v_{\Delta}= R_s\left[v_{\Delta}^{+}- v_{\Delta}\right]$$

where $v_{\Delta}=v_b-v_s$ is the velocity of the bow minus that of the string, $v_s=v_{s,l}^{+}+v_{s,l}^{-}=v_{s,r}^{+}+v_{s,r}^{-}$ is the string velocity in terms of traveling waves, $R_s$ is the wave impedance of the string (equal to the geometric mean of tension and density), and $R_b(v_{\Delta})$ is the friction coefficient for the bow against the string, i.e., bow force $F_b(v_{\Delta}) = R_b(v_{\Delta}) \cdot v_{\Delta}$ . (Force and velocity point in the same direction when they have the same sign.) Here, $v_{s,r}$ denotes transverse velocity on the segment of the bowed string to the right of the bow, and $v_{s,l}$ denotes velocity waves to the left of the bow. The corresponding normalized functions to be used in the Friedlander-Keller graphical solution technique are depicted in Fig.9.53.

Figure 9.53: Overlay of normalized bow-string friction curve $R_b(v_{\Delta })/R_s$ with the string ``load line'' $v_{\Delta }^{+}- v_{\Delta }$ . The ``capture'' and ``break-away'' differential velocity is denoted $v_{\Delta }^c$ . Note that increasing the bow force increases $v_{\Delta }^c$ as well as enlarging the maximum force applied (at the peaks of the curve).

In a bowed string simulation as in Fig.9.51, a velocity input (which is injected equally in the left- and right-going directions) must be found such that the transverse force of the bow against the string is balanced by the reaction force of the moving string. If bow-hair dynamics are neglected [177], the bow-string interaction can be simulated using a memoryless table lookup or segmented polynomial in a manner similar to single-reed woodwinds [435].

A derivation analogous to that for the single reed is possible for the simulation of the bow-string interaction. The final result is as follows.

$$v_{s,r}^{-} = v_{s,l}^{+}+ \hat\rho (v_{\Delta}^{+})\cdot v_{\Delta}^{+}$$

$$v_{s,l}^{-} = v_{s,r}^{+}+ \hat\rho (v_{\Delta}^{+})\cdot v_{\Delta}^{+}$$

where $v_{\Delta}^{+}\isdef v_b-(v_{s,r}^{+}+v_{s,l}^{+})$ , $v_b$ is bow velocity, and

$$\hat\rho (v_{\Delta}^{+})=\frac{r(v_{\Delta}(v_{\Delta}^{+}))}{1 + r(v_{\Delta}(v_{\Delta}^{+}))}$$

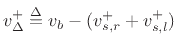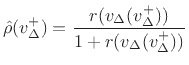
The impedance ratio is defined as $r(v_{\Delta})=0.25R_b(v_{\Delta})/R_s$ ,

Nominally, $R_b(v_{\Delta})$ is constant (the so-called static coefficient of friction) for $\vert v_{\Delta}\vert\leq v_{\Delta}^c$ , where $v_{\Delta }^c$ is both the capture and break-away differential velocity. For $\vert v_{\Delta}\vert>v_{\Delta}^c$ , $R_b(v_{\Delta})$ falls quickly to a low dynamic coefficient of friction. It is customary in the bowed-string physics literature to assume that the dynamic coefficient of friction continues to approach zero with increasing $\vert v_{\Delta}\vert>v_{\Delta}^c$ [311,95].

Figure 9.54: Simple, qualitatively chosen bow table for the digital waveguide violin.

Figure 9.54 illustrates a simplified, piecewise linear bow table $\hat\rho (v_{\Delta}^{+})$ . The flat center portion corresponds to a fixed reflection coefficient ``seen'' by a traveling wave encountering the bow stuck against the string, and the outer sections of the curve give a smaller reflection coefficient corresponding to the reduced bow-string interaction force while the string is slipping under the bow. The notation $v_{\Delta }^c$ at the corner point denotes the capture or break-away differential velocity. Note that hysteresis is neglected.