Semi-Implicit Backward Euler

The semi-implicit backward Euler method is defined by [558]

$$\underline{\hat{x}}(n) \isdefs \underline{\hat{x}}(n-1) + T\, \frac{f[n,\underline{\hat{x}}(n-1),\underline{u}(n)]}{1-T\,\ddot{\underline{\hat{x}}}(n-1)} \protect$$ (8.16)

where 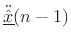$\ddot{\underline{\hat{x}}}(n-1)$ denotes an estimate of the second time derivative $\ddot{\underline{x}}(t)$ .