Relation of Lagrange and Sinc Interpolation

For an infinite number of equally spaced samples, with spacing $x_{k+1}-x_k = \Delta$, the Lagrangian basis polynomials converge to shifts of the sinc function, i.e.,

$$l_k(x) =$$   sinc$$\left(\frac{x-k\Delta}{\Delta}\right), \quad k=\ldots,-2,-1,0,1,2,\ldots$$

where

   sinc$$(x) \isdef \frac{\sin(\pi x)}{\pi x}$$

A simple argument is based on the fact that any analytic function is determined by its zeros and its value at one point. Since sinc$(x)$ is zero on all the integers except 0, and since sinc$(0)=1$, it must coincide with the infinite-order Lagrangian basis polynomial for the sample at $x=0$ which also has its zeros on the nonzero integers and equals $1$ at $x=0$.

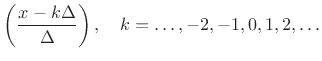
The equivalence of sinc interpolation to Lagrange interpolation was apparently first published by the mathematician Borel in 1899, and has been rediscovered many times since [315, p. 325].

A direct proof can be based on the equivalance between Lagrange interpolation and windowed-sinc interpolation using a ``binomial window'' [267,511]. That is, for a fractional sample delay of $D$ samples, multiply the shifted-by-$D$, sampled, sinc function

$$h_s(n) =$$   sinc$$(n-D) = \frac{\sin[\pi(n-D)]}{\pi(n-D)}$$

by a binomial window

$$w(n) = \left(\begin{array}{c}N\\ n\end{array}\right), \quad n=0,1,2,\ldots N$$

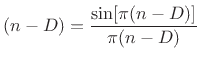
and normalize by [511]

$$C(D) = (-1)^N\frac{\pi(N+1)}{\sin(\pi D)}\left(\begin{array}{c}D\\ N+1\end{array}\right),$$

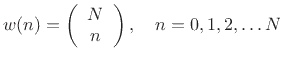
which normalizes the interpolating filter to have a unit $L_2$ norm, to obtain the $N$th-order Lagrange interpolating filter

$$h_D(n)=C(D)w(n)h_s(n), \quad n=0,1,2,\ldots,N$$

Since the binomial window converges to the Gaussian window as $N\to\infty$, and since the window gets wider and wider, approaching a unit constant in the limit, the convergence of Lagrange to sinc interpolation can be seen.