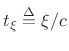 denote the time to propagate across the length of
the cone in one direction. As is well known [22], the reflectance
at the tip of an infinite cone is
denote the time to propagate across the length of
the cone in one direction. As is well known [22], the reflectance
at the tip of an infinite cone is
Let
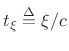 denote the time to propagate across the length of
the cone in one direction. As is well known [22], the reflectance
at the tip of an infinite cone is
denote the time to propagate across the length of
the cone in one direction. As is well known [22], the reflectance
at the tip of an infinite cone is ![]() for pressure waves. I.e., it
reflects like an open-ended cylinder. We ignore any absorption losses
propagating in the cone, so that the transfer function from the entrance of
the cone to the tip is
for pressure waves. I.e., it
reflects like an open-ended cylinder. We ignore any absorption losses
propagating in the cone, so that the transfer function from the entrance of
the cone to the tip is
![]() . Similarly, the transfer function from
the conical tip back to the entrance is also
. Similarly, the transfer function from
the conical tip back to the entrance is also
![]() . The complete
reflection transfer function from the entrance to the tip and back is then
. The complete
reflection transfer function from the entrance to the tip and back is then
| (C.176) |
We now want to interface the conical cap reflectance
![]() to the
cylinder. Since this entails a change in taper angle, there will be
reflection and transmission filtering at the cylinder-cone junction given
by Eq.(C.175) and Eq.(C.176).
to the
cylinder. Since this entails a change in taper angle, there will be
reflection and transmission filtering at the cylinder-cone junction given
by Eq.(C.175) and Eq.(C.176).
From inside the cylinder, immediately next to the cylinder-cone
junction shown in Fig.C.50, the reflectance of the conical cap is
readily derived from Fig.C.50b and Equations (C.175) and
(C.176) to be
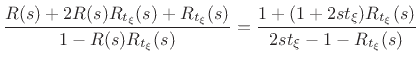 |
|||
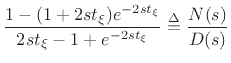 |
(C.177) |
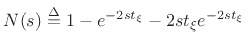 |
(C.178) |
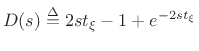 |
(C.179) |