For a rectangular cross-section of height ![]() and width
and width ![]() , area
, area
![]() , the area moment of inertia about the horizontal midline is
given by
, the area moment of inertia about the horizontal midline is
given by
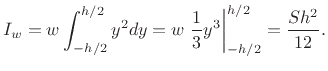
The radius of gyration about this axis is then
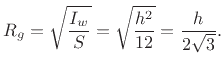
Similarly, the radius of gyration about a vertical axis passing through the center of the cross-section is
The radius of gyration can be thought of as the ``effective radius'' of the mass distribution with respect to its inertial response to rotation (``gyration'') about the chosen axis.
Most cross-sectional shapes (e.g., rectangular), have at least two radii of gyration. A circular cross-section has only one, and its radius of gyration is equal to half its radius, as shown in the next section.