For a circular cross-section of radius ![]() , Eq.(B.11) tells us
that the squared radius of gyration about any line passing through the
center of the cross-section is given by
, Eq.(B.11) tells us
that the squared radius of gyration about any line passing through the
center of the cross-section is given by
![\begin{eqnarray*}
R_g^2 &=& \frac{1}{\pi a^2} \int_{-a}^a dx \int_{-\sqrt{a^2-x^2}}^{\sqrt{a^2-x^2}} y^2 dy
\quad=\quad \frac{4}{\pi a^2} \int_0^a dx \int_0^{\sqrt{a^2-x^2}} y^2 dy\\ [10pt]
&=& \frac{4}{\pi a^2} \int_0^a \left[\frac{1}{3}(a^2-x^2)^{\frac{3}{2}}\right]dx
\quad=\quad \frac{4a}{3\pi} \int_0^a \left[1-\left(\frac{x}{a}\right)^2\right]^{\frac{3}{2}}dx\\ [10pt]
&& \qquad\hbox{[let $\sin(\theta)=x/a\,\,\Rightarrow\,\,dx=a\cos(\theta)d\theta$]}\\ [10pt]
&=& \frac{4a^2}{3\pi} \int_{0}^{\frac{\pi}{2}} \cos^4(\theta)d\theta.
\end{eqnarray*}](img2757.png)
Using the elementrary trig identity
![]() , we readily
derive
, we readily
derive
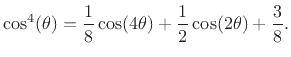
The first two terms of this expression contribute zero to the integral from 0 to
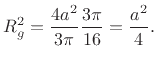
Thus, the radius of gyration about any midline of a circular cross-section of radius
For a circular tube in which the mass of the cross-section lies
within a circular annulus having inner radius ![]() and outer
radius
and outer
radius ![]() , the radius of gyration is given by
, the radius of gyration is given by