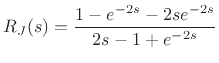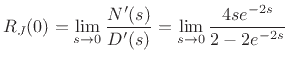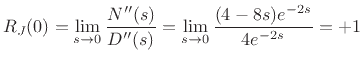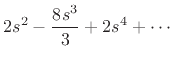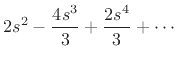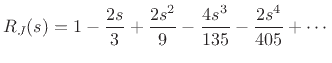Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
We know from the above that the denominator of the cone reflectance
has at least one root at  . In this subsection we investigate
this ``dc behavior'' of the cone more thoroughly.
. In this subsection we investigate
this ``dc behavior'' of the cone more thoroughly.
A hasty analysis based on the reflection and transmission filters in
Equations (C.175) and (C.176) might conclude that the reflectance
of the conical cap converges to 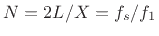 at dc, since
at dc, since 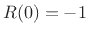 and
and  .
However, this would be incorrect. Instead, it is necessary to take the
limit as
.
However, this would be incorrect. Instead, it is necessary to take the
limit as
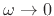 of the complete conical cap reflectance
of the complete conical cap reflectance 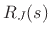 :
:
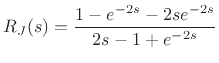 |
(C.186) |
We already discovered a root at  in the denominator in the context of
the preceding stability proof. However, note that the numerator also goes
to zero at
in the denominator in the context of
the preceding stability proof. However, note that the numerator also goes
to zero at  . This indicates a pole-zero cancellation at dc. To find
the reflectance at dc, we may use L'Hospital's rule to obtain
. This indicates a pole-zero cancellation at dc. To find
the reflectance at dc, we may use L'Hospital's rule to obtain
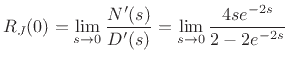 |
(C.187) |
and once again the limit is an indeterminate 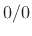 form.
We therefore apply L'Hospital's rule again to obtain
form.
We therefore apply L'Hospital's rule again to obtain
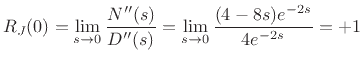 |
(C.188) |
Thus, two poles and zeros cancel at dc, and the dc reflectance is 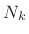 , not
, not
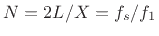 as an analysis based only on the scattering filters would indicate.
From a physical point of view, it makes more sense that the cone should
``look like'' a simple rigid termination of the cylinder at dc, since its
length becomes small compared with the wavelength in the limit.
as an analysis based only on the scattering filters would indicate.
From a physical point of view, it makes more sense that the cone should
``look like'' a simple rigid termination of the cylinder at dc, since its
length becomes small compared with the wavelength in the limit.
Another method of showing this result is to form a Taylor series expansion
of the numerator and denominator:
Both series begin with the term 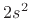 which means both the numerator
and denominator have two roots at
which means both the numerator
and denominator have two roots at  . Hence, again the conclusion
is two pole-zero cancellations at dc. The series for the conical cap
reflectance can be shown to be
. Hence, again the conclusion
is two pole-zero cancellations at dc. The series for the conical cap
reflectance can be shown to be
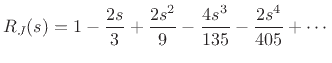 |
(C.191) |
which approaches 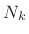 as
as 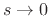 .
.
An alternative analysis of this issue is given by Benade in [37].
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() . In this subsection we investigate
this ``dc behavior'' of the cone more thoroughly.
. In this subsection we investigate
this ``dc behavior'' of the cone more thoroughly.
![]() at dc, since
at dc, since ![]() and
and ![]() .
However, this would be incorrect. Instead, it is necessary to take the
limit as
.
However, this would be incorrect. Instead, it is necessary to take the
limit as
![]() of the complete conical cap reflectance
of the complete conical cap reflectance ![]() :
: