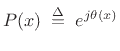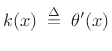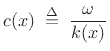Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
More General One-Parameter Waves
The wave impedance derivation above made use of known properties of waves
in cones to arrive at the wave impedances in the two directions of travel
in cones. We now consider how this solution might be generalized to
arbitrary bore shapes. The momentum conservation equation is already
applicable to any wavefront area variation 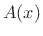 :
:
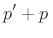
ln
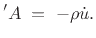
As we did for vibrating strings (§C.3.4), suppose the
pressure is sinusoidally driven so that we have
where 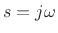 ,
,
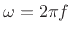 , and
, and 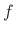 is the driving frequency.
The partial derivatives become
is the driving frequency.
The partial derivatives become
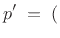
ln

Substituting into the momentum equation gives
Because the medium is linear and time-invariant, the velocity 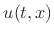 must
be of the form
must
be of the form
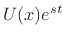 , and we can define the spatially instantaneous
wave impedance as
, and we can define the spatially instantaneous
wave impedance as
The corresponding instantaneous wave admittance is then
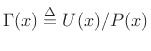 .
Then
.
Then
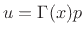 , and the momentum equation becomes
, and the momentum equation becomes
ln
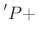
ln
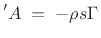
Solving for the wave impedance gives
Expressing 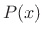 in exponential form as
in exponential form as
where 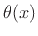 may be complex, we may define the instantaneous
spatial frequency (wavenumber) as
may be complex, we may define the instantaneous
spatial frequency (wavenumber) as
and since
ln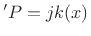 , we have
, we have
Defining the spatially instantaneous phase velocity as
we have
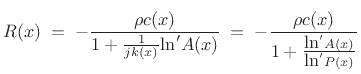 |
(C.172) |
This reduces to the simple case of the uniform waveguide when the
logarithmic derivative of cross-sectional area 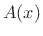 is small compared
with the logarithmic derivative of the amplitude
is small compared
with the logarithmic derivative of the amplitude 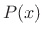 which
is proportional to the instantaneous spatial frequency.
A traveling wave solution interpretation makes sense when
the instantaneous wavenumber
which
is proportional to the instantaneous spatial frequency.
A traveling wave solution interpretation makes sense when
the instantaneous wavenumber 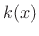 is approximately real, and
the phase velocity
is approximately real, and
the phase velocity 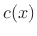 is approximately constant over a number of
wavelengths
is approximately constant over a number of
wavelengths
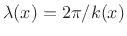 .
.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() :
:
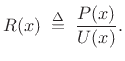
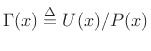 .
Then
.
Then