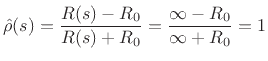
The force-wave reflectance of an infinite impedance (rigid wall or ``open circuit'') is
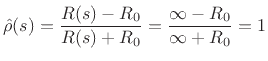
Similarly, the force-wave reflectance of a zero impedance (free termination, frictionless surface, or ``short circuit'') is
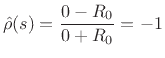
For velocity waves, we obtain the opposite results: rigid terminations are inverting, and free terminations are non-inverting.