In statistical thermodynamics [176,139], it
is derived that each molecular degree of freedom contributes ![]() to
the molar heat capacity (or specific heat) of an ideal
gas, where
to
the molar heat capacity (or specific heat) of an ideal
gas, where ![]() is the ideal gas constant.
is the ideal gas constant.
An ideal monatomic gas molecule (negligible spin) has only
three degrees of freedom: its kinetic energy in the three spatial
dimensions. Therefore,
![]() . This means we expect
. This means we expect
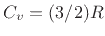
a result that agrees well with experimental measurements [139].
For an ideal diatomic gas molecule such as air, which can be
pictured as a ``bar bell'' configuration of two rubber balls, two
additional degrees of freedom are added, both associated with spinning
the molecule about an axis orthogonal to the line connecting the
atoms, and piercing its center of mass. There are two such
axes. Spinning about the connecting axis is neglected because the
moment of inertia is so much smaller in that case. Thus, for diatomic
gases such as dry air (![]() % nitrogen
N
% nitrogen
N![]() and oxygen
O
and oxygen
O![]() ),
we expect
),
we expect
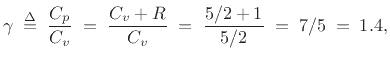
as observed to a good degree of approximation at normal temperatures. At high temperatures, new degrees of freedom appear associated with vibrations in the molecular bonds. (For example, the ``bar bell'' can vibrate longitudinally.) However, such vibrations are ``frozen out'' at normal room temperatures, meaning that their (quantized) energy levels are too high and spaced too far apart to be excited by room temperature collisions [139, p. 147].B.32