Evanescent Wave due to Total Internal Reflection

Note that if $c_1 < c_2 \vert\sin(\theta_1^+)\vert$ , the horizontal component of the wavenumber in medium 2 becomes imaginary. In this case, the wave in medium 2 is said to be evanescent, and the wave in medium 1 undergoes total internal reflection (no power travels from medium 1 to medium 2). The evanescent-wave amplitude decays exponentially to the right and oscillates ``in place'' (like a standing wave). ``Tunneling'' is possible given a medium 3 beyond medium 2 in which wave propagation resumes.

To show explicitly the exponential decay and in-place oscillation in an evanescent wave, express the imaginary wavenumber as 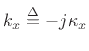$k_x\isdef -j\kappa_x$ . Then we have

$$\begin{eqnarray*} p(t,\underline{x}) &=& \cos\left(\omega t - \underline{k}^T\underline{x}\right)\;=\; \mbox{re\ensuremath{\left\{e^{j(\omega t - k_x x - k_y y )}\right\}}}\\ [5pt] &=& \mbox{re\ensuremath{\left\{e^{j(\omega t - k_y y)} e^{-j k_x x}\right\}}},\quad \mbox{($k_x\isdef -j\kappa_x$)}\\ [5pt] &\isdef & \mbox{re\ensuremath{\left\{e^{j(\omega t - k_y y)} e^{-k_x x}\right\}}}\\ [5pt] &=& e^{-k_x x} \cos(\omega t - k_y y). \end{eqnarray*}$$

Thus, an imaginary wavenumber corresponds to an exponentially decaying evanescent wave. Note that the time dependence (cosine term) applies to all points to the right of the boundary. Since evanescent waves do not really ``propagate,'' it is perhaps better to speak of an ``evanescent acoustic field'' or ``evanescent standing wave'' instead of ``evanescent waves''.

For more on the physics of evanescent waves and tunneling, see [297].