Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
A cubic nonlinearity, as well as any odd distortion
law,10.2 generates only odd-numbered harmonics (like in a square
wave). For best results, and in particular for tube distortion
simulation [31,398], it has been argued that some
amount of even-numbered harmonics should also be present.
Breaking the odd symmetry in any way will add even-numbered harmonics
to the output as well. One simple way to accomplish this is to add an
offset to the input signal, obtaining
where 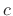 is some small constant. (Signals
is some small constant. (Signals 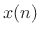 in practice are
typically constrained to be zero mean by one means or another.)
in practice are
typically constrained to be zero mean by one means or another.)
Another method for breaking the odd symmetry is to add some
square-law nonlinearity to obtain
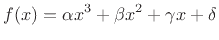 |
(10.6) |
where  controls the amount of square-law distortion in the more
general third-order polynomial. The square-law is the most gentle
nonlinear distortion in existence, adding only some second harmonic to
a sinusoidal input signal. The constant
controls the amount of square-law distortion in the more
general third-order polynomial. The square-law is the most gentle
nonlinear distortion in existence, adding only some second harmonic to
a sinusoidal input signal. The constant 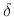 can be set to zero
the mean, on average; if the input signal
can be set to zero
the mean, on average; if the input signal 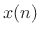 is zero-mean with
variance is 1, then
is zero-mean with
variance is 1, then
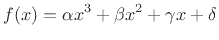 will cancel the nonzero mean
induced by the squaring term
will cancel the nonzero mean
induced by the squaring term  . Typically, the output of any
audio effect is
mixed with the original input signal to allow easy control over
the amount of effect. The term
. Typically, the output of any
audio effect is
mixed with the original input signal to allow easy control over
the amount of effect. The term 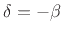 can be used for this,
provided the constant gains for
can be used for this,
provided the constant gains for 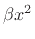 and
and 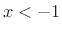 are modified
accordingly, or
are modified
accordingly, or  is hard-clipped to the desired range at the input.
is hard-clipped to the desired range at the input.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]