Eigenstructure

Starting with the defining equation for an eigenvector $\underline{e}$ and its corresponding eigenvalue $\lambda$ ,

$$\mathbf{A}\underline{e}_i = {\lambda_i}\underline{e}_i,\quad i=1,2$$

we get, using Eq.(C.158),

$$\left[\begin{array}{cc} gc & c-1 \\ [2pt] gc+g & c \end{array}\right] \left[\begin{array}{c} 1 \\ [2pt] \eta_i \end{array}\right] = \left[\begin{array}{c} {\lambda_i} \\ [2pt] {\lambda_i}\eta_i \end{array}\right]. \protect$$ (C.161)

We normalized the first element of $\underline{e}_i$ to 1 since $g\underline{e}_i$ is an eigenvector whenever $\underline{e}_i$ is. (If there is a missing solution because its first element happens to be zero, we can repeat the analysis normalizing the second element to 1 instead.)

Equation (C.162) gives us two equations in two unknowns:

$$gc+\eta_i(c-1) = {\lambda_i} \protect$$ (C.162)

$$g(1+c) +c\eta_i = {\lambda_i}\eta_i$$ (C.163)

Substituting the first into the second to eliminate ${\lambda_i}$ , we get

$$\begin{eqnarray*} g+gc+c\eta_i &=& [gc+\eta_i(c-1)]\eta_i = gc\eta_i + \eta_i^2 (c-1)\\ \,\,\Rightarrow\,\,\eta_i &=& \frac{c(g-1)}{2(1-c)} \pm \sqrt{\frac{c^2(1-g)^2 - 4g(1-c^2)}{(c-c)^2}}\\ &=& \frac{(g-1)c}{2(1-c)} \pm j\sqrt{g\left(\frac{1+c}{1-c}\right) - \frac{c^2(1-g)^2}{4(1-c)^2}}. \end{eqnarray*}$$

As $g$ approaches $1$ (no damping), we obtain

$$\eta_i = \pm j\sqrt{\frac{1+c}{1-c}} \qquad \hbox{(when $g=1$)}.$$

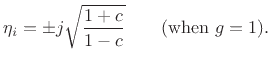
Thus, we have found both eigenvectors:

$$\begin{eqnarray*} \underline{e}_1&=&\left[\begin{array}{c} 1 \\ [2pt] \eta \end{array}\right],\qquad \underline{e}_2=\left[\begin{array}{c} 1 \\ [2pt] -\eta \end{array}\right], \quad \hbox{where}\\ \eta&\isdef & \frac{(g-1)c}{2(1-c)} + j\sqrt{g\left(\frac{1+c}{1-c}\right) - \frac{c^2(1-g)^2}{4(1-c)^2}} \end{eqnarray*}$$

They are linearly independent provided $\eta\neq0$ . In the undamped case ($g=1$ ), this holds whenever $c\neq -1$ . The eigenvectors are finite when $c\neq 1$ . Thus, the nominal range for $c$ is the interval $c\in(-1,1)$ .

We can now use Eq.(C.163) to find the eigenvalues:

$$\begin{eqnarray*} {\lambda_i}&=& gc+ \eta_i(c-1)\\ &=& gc+ \frac{(1-g)c}{2}\pm \sqrt{\left(\frac{c(1-g)}{2}\right)^2 - g (1-c^2)}\\ &=& c\left(\frac{1+g}{2}\right) \pm j\sqrt{g(1-c^2) - \left[\frac{c(1-g)}{2}\right]^2} \protect \end{eqnarray*}$$