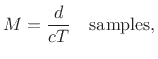Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
We may regard the delay-line memory itself as the fixed ``air'' which
propagates sound samples at a fixed speed 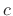 (
(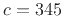 meters per
second at
meters per
second at 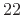 degrees Celsius and 1 atmosphere). The input signal
degrees Celsius and 1 atmosphere). The input signal
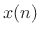 can be associated with a sound source, and the output signal
can be associated with a sound source, and the output signal
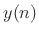 (see Fig.2.1 on page
(see Fig.2.1 on page ![[*]](../icons/crossref.png) ) can be associated with
the listening point. If the listening point is
) can be associated with
the listening point. If the listening point is 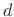 meters away from
the source, then the delay line length
meters away from
the source, then the delay line length  needs to be
needs to be
where 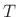 denotes the discrete-time sampling interval. In other
words, the number of samples delay is the propagation distance
denotes the discrete-time sampling interval. In other
words, the number of samples delay is the propagation distance 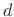 divided by
divided by 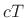 , the distance sound propagates in one sampling
interval. In practice, rounding
, the distance sound propagates in one sampling
interval. In practice, rounding 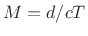 to the nearest integer
causes no audible difference, unless the echo time is so short that
the system is not really perceived as an echo (we'll learn about
``comb filters'' in §2.6 below).
to the nearest integer
causes no audible difference, unless the echo time is so short that
the system is not really perceived as an echo (we'll learn about
``comb filters'' in §2.6 below).
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() (
(![]() meters per
second at
meters per
second at ![]() degrees Celsius and 1 atmosphere). The input signal
degrees Celsius and 1 atmosphere). The input signal
![]() can be associated with a sound source, and the output signal
can be associated with a sound source, and the output signal
![]() (see Fig.2.1 on page
(see Fig.2.1 on page ![]() ) can be associated with
the listening point. If the listening point is
) can be associated with
the listening point. If the listening point is ![]() meters away from
the source, then the delay line length
meters away from
the source, then the delay line length ![]() needs to be
needs to be