Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Angular Motion
in the Space-Fixed Frame
Let's now consider angular motion in the presence of linear motion of
the center of mass. In general, we have [272]
where the sum is over all mass particles in the rigid body, and
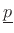 denotes the vector linear momentum for each particle. That
is, the angular momentum is given by the tangential component of the
linear momentum times the associated moment arm. Using the chain rule
for differentiation, we find
denotes the vector linear momentum for each particle. That
is, the angular momentum is given by the tangential component of the
linear momentum times the associated moment arm. Using the chain rule
for differentiation, we find
However,
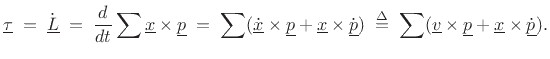 , so that
, so that
which is the sum of moments of all external forces.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]